Существуют ли такие три различных поло­жительных числа

Существуют ли такие три различных поло­жительных числа, которые одновременно образуют арифмети­ческую и геометрическую прогрессии?

Решение:

Пусть m₁, m₂, m_{3 —} различные положительные числа, которые являются последовательными членами ариф­метической и геометрической прогрессий. Тогда верны равен­ства

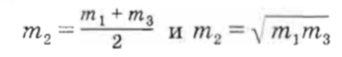
Приравняв правые части этих равенств, имеем верное равенство

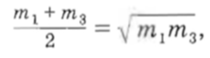
откуда получаем

и, значит, m₁ = m₃. Но это противоречит условию. Значит, та­кие числа не существуют.

Ответ: не существуют.