Сумма первых четырех членов геометриче ской прогрессии равна 120. Известно, что ее второй, третий и четвертый члены различны и являются соответственно пер вым, пятым и седьмым членами арифметической прогрессии. Найти первый член геометрической прогрессии и первый член арифметической прогрессии.
Решение:
Пусть (аn) — арифметическая прогрессия с разностью d, а (bn) — геометрическая прогрессия со знаменателем q. Тогда по условию имеем:
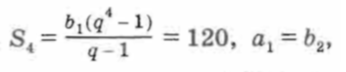
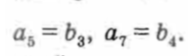
Использовав формулы n-го члена арифметической и n-го члена геометрической прогрессий, получим систему уравнений
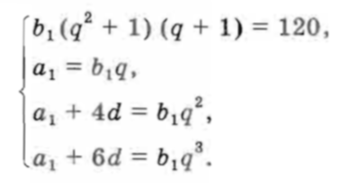
Заменив в 3-м и 4-м уравнениях а1 на b1q и выразив из них d, получим
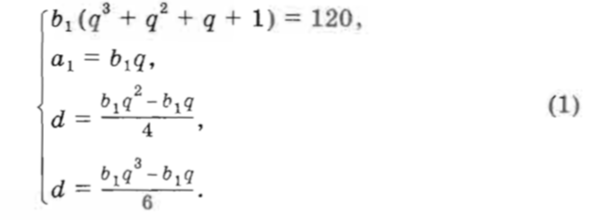
Приравняв правые части двух последних равенств, получим новое уравнение, обе части которого можно разделить на b1q/2 После чего имеем:
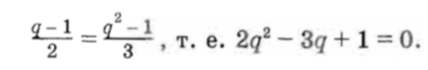
Решив это уравнение, получим
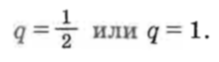
Поскольку по условию члены геометрической прогрессии различны , то q = 1/2.
Из первого уравнения системы (1) находим
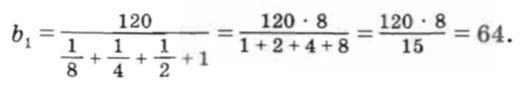
Из второго уравнения системы (1) находим:
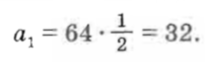
Ответ: b1 = 64; а1 = 32.