Задачи по арифметической и геометрической прогрессии для 10 класса

3.99. В арифметической прогрессии 11 различных членов. Первый, пятый и одиннадцатый члены составляют гео­ метрическую прогрессию. Найдите все члены арифме­тической прогрессии, если ее первый член равен 24.

Ответ: 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54.

3.100. Первый член арифметической прогрессии (а_n) равен 1, а сумма ее первых семи членов равна 91. Найдите деся­тый член геометрической прогрессии (b_n), если а₁ = b₁ и a₇ = b₇.

Ответ: ±125.

3.101. Задайте формулой n-го члена арифметическую и геомет­рическую прогрессии, если известно, что разность ариф­метической прогрессии отлична от нуля, первый член каждой прогрессии равен 2, третьи члены обеих про­грессий равны между собой, а одиннадцатый член ариф­метической прогрессии равен пятому члену геометри­ческой.

Ответ: a_n = 3n — 1, b_n = 2 · (2)^n-1

3.102. Первый член арифметической прогрессии с неравными членами и первый член геометрической прогрессии рав­ны 3. Второй член арифметической прогрессии больше второго члена геометрической на 6, а третьи члены про­грессий одинаковы. Задайте эти прогрессии формулами n-го члена.

Ответ: a_n = 12n — 9, b_n = 3ⁿ

3.103. Три различных числа a, b, c, сумма которых равна 52, являются тремя последовательными членами геометри­ческой прогрессии. Одновременно эти три числа a, b, c являются соответственно четвертым, шестым и двена­дцатым членами арифметической прогрессии. Найдите числа a, b, c.

Ответ: a = 4, b = 12, c = 36.

3.104. Три различных числа a, b, c, сумма которых равна 147, являются тремя последовательными членами геометри­ческой прогрессии. Одновременно эти три числа a, b, c являются соответственно третьим, десятым и тридцать восьмым членами арифметической прогрессии. Найди­ те числа a, b, c.

Ответ: a = 7, b = 28, c = 112.

3.105. Сумма пяти первых членов геометрической прогрессии равна 62. Известно, что пятый, восьмой и одиннадца­ тый члены этой прогрессии различны и являются соот­ ветственно первым, вторым и десятым членами ариф­метической прогрессии. Найдите первый член геомет­рической прогрессии.

Ответ: 2.

3.106. Числа b1, b2, b3, b4, b5, сумма которых равна 62, явля­ ются первыми пятью членами геометрической прогрес­ сии, а числа b3, 1,25b4, b5 — последовательными члена­ми арифметической прогрессии. Найдите первый член и знаменатель геометрической прогрессии.

Ответ: b1 = 32, q = 0,5 или b1 = 2, q = 2.

3.107. Сумма трех чисел, составляющих арифметическую про­грессию, равна 33. Если к первому члену прибавить 1, к третьему 2, а от второго отнять 1, то полученные числа составят геометрическую прогрессию. Найдите эти числа.

Ответ: 19; 11; 3 или 4; 11; 18.

3.108. Сумма трех чисел, составляющих арифметическую про­грессию, равна 21. Если к ним соответственно приба­вить 2, 3 и 9, то полученные числа составят геометри­ческую прогрессию. Найдите эти числа.

Ответ: 18; 7; -4 или 3; 7; 11.

3.109. Сумма трех чисел, составляющих геометрическую про­грессию, равна 65. Если от меньшего из этих чисел от­нять 1, а от большего 19, то полученные числа составят арифметическую прогрессию. Найдите эти числа.

Ответ: 5; 15; 45.

3.110. Найдите четыре числа, из которых первые три состав­ляют арифметическую, а последние три — геометри­ческую прогрессии, если сумма двух крайних чисел равна 22, а сумма двух средних чисел равна 20.

Ответ: 4; 8; 12; 18 или 17,5; 12,5; 7,5; 4,5.

3.111*. Три числа составляют геометрическую прогрессию. Если ко второму числу прибавить 8, то эти числа соста­вят арифметическую прогрессию. Если затем к третьему числу прибавить 64, то полученные числа вновь соста­вят геометрическую прогрессию. Найдите исходные числа.

Ответ: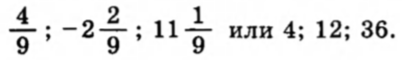

3.112*. Даны арифметическая и геометрическая прогрессии. Два первых члена геометрической прогрессии совпада­ ют соответственно с первым и вторым членами арифметической прогрессии, и их сумма равна 24, а третий член геометрической прогрессии больше третьего члена арифметической прогрессии на 8. Задайте эти прогрес­сии формулами n-го члена.

Ответ: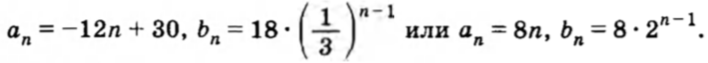

3.113*. Найдите числа, одновременно являющиеся членами арифметической прогрессии 12, 15, 18, … и геометри­ческой прогрессии 1, 3, 9, …, если каждая из этих про­грессий содержит по 100 членов.

Ответ: 27; 81; 243

3.114*. Пусть a1, а2, а3 — конечная арифметическая прогрес­сия, разность которой не равна нулю. Известно, что а1а2, а2а3, а3а1 — конечная геометрическая прогрессия. Най­дите ее знаменатель.

Ответ: -2.

3.115. 1) В какую сумму обратится вклад в 200 000 р., поло­женный в банк на 5 лет, если банк ежегодно увеличи­вает имеющуюся на счету сумму на 2 %?
2) Банк ежегодно увеличивает имеющуюся на счету сумму на 3 %. Внесено 500 000 р. Какой станет сумма вклада через 2 года?

Ответ: 1) 220 816,16 р.; 2) 530 450 р.

3.116. 1) Какой вклад надо внести в банк под 3% годовых, чтобы через 3 года получить 458 000 р.?
2) Вкладчик внес в банк 600 000 р., а через год у него на счету оказалось 642 000 р. Под какие проценты был внесен вклад?

Ответ: 1) 419 135 р.; 2) 7%.

3.117. 1) В городе 200 тыс. жителей. Сколько жителей в нем будет через 10 лет, если ежегодный прирост населения в среднем составляет 4 % ?
2) В настоящее время в городе проживают 400 тыс. че­ловек. Какой была численность населения 5 лет назад, если ежегодный прирост населения города составлял в среднем 2,5%?

Ответ: 1) 296 049; 2) 354 000.

3.118. Члены арифметической (а_n) и геометрической (b_n) про­грессий удовлетворяют условиям а₄₀ = b₄₀ > 0, а₆₀ = b₆₀ > 0. Сравните члены прогрессий а₅₀ и b₅₀ (а₄₀ ≠ а₆₀).

Ответ: a₅₀ > b₅₀.